

July 20, 2005 ... Email from Darlene
Why skies are blue instead of purple MSNBC, July 20, 2005

Blue Skies Only In the Eye of the Beholder Live Science, July 20, 2005
While scientists have the daytime sky figured out, they are still trying to understand why the night time sky is black, instead of full of light. Cosmologists and physicists have wondered for many years about this, and have yet to come up with an accepted explanation for what they call Olber's Paradox.
My personal theory ... Being able to see those stars and planets against the black background is important to us on a conscious level. Just think how man might have evolved if he had not been able to view the night sky as we see it.

Olbers' Paradox, described by the German astronomer Heinrich Wilhelm Olbers in 1823 (but not published by Bode until 1826), and earlier by Johannes Kepler in 1610, and Halley and Cheseaux in the 18th century, is the paradoxical observation that the night sky is dark, when in a static infinite universe the night sky ought to be bright. It is one of the pieces of evidence for a non-static Universe such as the current Big Bang model. This paradox is sometimes also known as the "dark night sky paradox".
Assumptions
If the universe is assumed to contain an infinite number of uniformly distributed luminous stars, then:
2) Every line of sight should terminate eventually on the surface of a star
3) Every point in the sky should be as bright as the surface of a star. Looking at trees within a big flat wood in direction of the horizon shows the effect: The mass of dark trees will hide the horizon (imagine yourself trees now as lights).
The further away one looks, the older the image viewed by the observer. For stars to appear "uniformly distributed" in space, the light from the stars must have been emitted from places where the stellar density of the region at the time of emission was the same as the current local stellar density. Simple interpretation of Olber's paradox assumes that there were no dramatic changes in the homogeneous distribution of stars in that time. This implies that if the universe is infinitely old and infinitely large, the flux received by stars would be infinite.
Kepler saw this as an argument for a finite observable universe, or at least for a finite number of stars. The current scientific consensus is that effects of general relativity relating to the Big Bang and the finite age of the Universe do indeed give a finite size for the observable universe, but that it is the astronomical redshift relationship which really explains the dark sky at night.
The works of experts suggests that if just the assumption that the universe is infinite is dropped the paradox still holds. Though the sky would not be infinitely bright, every point in the sky would still be like the surface of a star.
A more precise way to look at this is to place earth in the centre of a "sphere". If the universe were homogeneous and infinite, then at a distance, r, away from the earth, the shell of the sphere would have a certain flux (viewed from earth) due to the individual flux of the stars on the shell (brightness) and also the number of stars in the shell (cumulative flux). When an observer from earth looks to a farther distance to another shell, r + x, the number of stars increases by the square of the distance, while the flux decreases by the inverse squared. Comparing the total brightness of the first shell to the second shell, one notices that both shells have equal flux, since the flux of each individual star decreases due to distance but is equally made up for by the number of stars. This means that no matter how far away an observer on earth views the sky, the brightness of each consecutive shell would not diminish, rather they would be equal. If the universe were infinite (age and volume) and had a regular distribution of stars, then there will be an infinite number of such shells and infinite amount of time for the light to reach earth (infinite flux) as long as the earth remains, effectively meaning that there would never be night on earth.
In order to explain Olbers' paradox, one must reason a way how the sky will not appear as bright as the circle of our Sun in every point in the sky, that is to say, the relatively low brightness in relation to the circle of our Sun needs to be accounted for.
Finite speed of light
As we look further out in space we see further back in history. Therefore, the further the distance, the longer light takes to travel. However the speed of light has very little to do with the energy density and broadness of light received at the majority of points of the universe.
The origin of all light is a finite distance away.
It is possible to conceive of an alternate universe where every possible line of sight is finite, and yet have a sky which is as bright as the circle of the sun in all of its points. According to the Big Bang theory, the skies of many places were much brighter in the past, especially in the first few seconds of the timeline of the universe. It is certain in such a scenario that all points of the local sky would be brighter than the circle of the sun, despite the finite and even more limited range that emitted light travelled as far as that prehistoric era went; this implies that a finity of illuminated space does not explain why sky is so dark.
Finite age of Stars
Stars have a finite age and always a finite power, thereby implying that they have a finite impact on a sky's light field density. Finity of the influence from stars of any topographical arrangement alone does not imply that our sky will be darker than the circle of the sun in most areas of our sky. If the collective finity of such influences were great enough at a given point, all points of the sky for that point would be as bright as the stars. Despite being neither a sufficient nor a necessary explanation of the darkness of the sky, the finite age of stars is considered by some to be a reason for the dark sky, and accordingly, is seen as a solution to Olbers' paradox.
Expanding space from an opaque singularity
While the finity of distal ranges of all received light's origins does not by itself solve the paradox, the mainstream theory of the universe, called the Big Bang Theory, involves an expanding space which can cause the energy of emitted light to be reduced via redshift, in spite of the assumed overall homogeneity of the distribution of luminous matter at the largest scales. More specifically, the extremely intense levels of radiation from the Big Bang have been redshifted to microwave wavelengths as a result of the cosmic expansion and thus forming the cosmic microwave background radiation. This explains the relatively low light densities present in the majority of our sky despite the nature of the bright additive radiation field in its early history.
Since the universe is thought of as coming from a singularity, the expansion of the universe also limits the size of the observable universe, which means that light cannot come from beyond the singularity, effectively prohibiting light to come from yet further distances. The particle horizon creates the optical effect of living in a finite universe. In essence, expanding space from a singularity is a way to explain as to why the light field in all parts of the sky, even in the context of a homogeneous distribution of stars, does not mirror the brightness of the circle of our Sun. In other words, a light field of finite density in space expanding finitely from an opaque singularity explains low light density below that of the light density surrounding higher concentrations of luminous matter such as our nearby Sun, and thereby resolves Olbers' paradox.
An alternative explanation which is sometimes suggested by non-scientists is that the universe is not transparent, and the light from distant stars is blocked by intermediate dark stars or absorbed by dust or gas, so that there is a bound on the distance from which light can reach the observer. However, this reasoning would not resolve the paradox given the following argument: According to the second law of thermodynamics there can be no material hotter than its surroundings that does not give off radiation. There is no material which can be uniformly distributed through space and yet able to absorb more radiation than it emits without increasing in temperature. Energy must be conserved, per the first law of thermodynamics. Therefore, the intermediate matter would heat up and soon reradiate the energy (possibly at different wavelengths). This would again result in intense uniform radiation as bright as the collective of stars themselves, which is not observed. Although, if there existed a particle which immediately converted electromagnetic energy into visible matter, these pockets in space of the material could continue to grow and go unnoticed.
A different resolution, which does not rely on the Big Bang theory, was offered in 1974 by Beno”t Mandelbrot. He postulated that if the stars in the universe were fractally distributed (e.g. like a Cantor dust), it would not be necessary to rely on the Big Bang theory to explain Olbers' Paradox. This model would not rule out a Big Bang, but would allow for a dark sky even if the Big Bang had not occurred. This is merely a demonstration of the consequences of fractal theory as a sufficient, but not necessary, resolution of the paradox.
The idea of a hierarchical cosmology - what would now be called a fractal cosmology, is not Mandelbrot's invention - notably, it had been proposed in 1908, decades earlier, by Carl Charlier.
Mathematically, the light received from stars as a function of distance from stars in a hypothetical fractal cosmos can be described via the following function of integration:
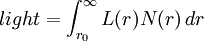
Fractal Cosmology as a Myth
The component of the Big Bang Theory which involves an expanding space from a singularity is a more widely accepted explanation for Olbers' Paradox - among other things. As for its inclusion in the Big Bang Theory, the cosmological principle and timeline of the universe have prevented or disallowed general cosmologists to find evidence to support a fractal distribution over the scales of billion light years, since the assumption of a galactic evolution of a homogeneous universe does not permit coherent observations of discrete 10+ billion light year structures if these structures' gradient energy-density variations are largely detectable along the direction of our viewing of the sky (as the "perceived" evolution of galaxies) - but not otherwise. That is to imply that, observations of billion parsec structures staring at the face of cosmological observers may go unnoticed, as energy-density gradients of this spatial magnitude along planes perpendicular to the line of sight may be rather shallow, creating an apparent topological homogeneity like that expected under cosmological principle. For this reason, it is easy for some to regard fractal cosmology as a myth, rather than as an eminent possibility.