

�Chaos theory is the field of study in mathematics that studies the behavior of dynamical systems that are highly sensitive to initial conditions - a response popularly referred to as the butterfly effect. Small differences in initial conditions (such as those due to rounding errors in numerical computation) yield widely diverging outcomes for such dynamical systems, rendering long-term prediction impossible in general.

This happens even though these systems are deterministic, meaning that their future behavior is fully determined by their initial conditions, with no random elements involved. In other words, the deterministic nature of these systems does not make them predictable. This behavior is known as deterministic chaos, or simply chaos. The theory was summarized by Edward Lorenz as:
Chaotic behavior exists in many natural systems, such as weather and climate. It also occurs spontaneously in some systems with artificial components, such as road traffic This behavior can be studied through analysis of a chaotic mathematical model, or through analytical techniques such as recurrence plots and Poincare maps. Chaos theory has applications in several disciplines, including meteorology, sociology, physics, environmental science, computer science, engineering, economics, biology, ecology, and philosophy.

Scientists have unveiled a way of achieving a shutter speed that's a mere trillionth of a second, or 250 million times faster than those digital cameras. That makes it capable of capturing something very important in materials science: dynamic disorder. Simply put, it's when clusters of atoms move and dance around in a material in specific ways over a certain period - triggered by a vibration or a temperature change, for example. It's not a phenomenon that we fully understand yet, but it's crucial to the properties and reactions of materials.

The roots of chaos theory date back to about 1900, in the studies of Henri Poincare on the problem of the motion of three objects in mutual gravitational attraction, the so-called three-body problem. Poincare found that there can be orbits which are nonperiodic, and yet not forever increasing nor approaching a fixed point. Later studies, also on the topic of nonlinear differential equations, were carried out by G.D. Birkhoff, A.N. Kolmogorov, M.L. Cartwright, J.E. Littlewood, and Stephen Smale. Except for Smale, who was perhaps the first pure mathematician to study nonlinear dynamics, these studies were all directly inspired by physics: the three-body problem in the case of Birkhoff, turbulence and astronomical problems in the case of Kolmogorov, and radio engineering in the case of Cartwright and Littlewood. Although chaotic planetary motion had not been observed, experimentalists had encountered turbulence in fluid motion and nonperiodic oscillation in radio circuits without the benefit of a theory to explain what they were seeing.
Chaos theory progressed more rapidly after mid-century, when it first became evident for some scientists that linear theory, the prevailing system theory at that time, simply could not explain the observed behavior of certain experiments like that of the logistic map. The main catalyst for the development of chaos theory was the electronic computer. Much of the mathematics of chaos theory involves the repeated iteration of simple mathematical formulas, which would be impractical to do by hand. Electronic computers made these repeated calculations practical. One of the earliest electronic digital computers, ENIAC, was used to run simple weather forecasting models.
An early pioneer of the theory was Edward Lorenz whose interest in chaos came about accidentally through his work on weather prediction in 1961. Lorenz was using a basic computer, a Royal McBee LGP-30, to run his weather simulation. He wanted to see a sequence of data again and to save time he started the simulation in the middle of its course. He was able to do this by entering a printout of the data corresponding to conditions in the middle of his simulation which he had calculated last time.
Chaos theory is applied in many scientific disciplines, including: geology, mathematics, microbiology, biology, computer science, economics, engineering, finance, meteorology, philosophy, physics, politics, population dynamics, psychology, and robotics.
Chaotic behavior has been observed in the laboratory in a variety of systems, including electrical circuits, lasers, oscillating chemical reactions, fluid dynamics, and mechanical and magneto-mechanical devices, as well as computer models of chaotic processes. Observations of chaotic behavior in nature include changes in weather, the dynamics of satellites in the solar system, the time evolution of the magnetic field of celestial bodies, population growth in ecology, the dynamics of the action potentials in neurons, and molecular vibrations. There is some controversy over the existence of chaotic dynamics in plate tectonics and in economics.
Chaos theory is currently being applied to medical studies of epilepsy, specifically to the prediction of seemingly random seizures by observing initial conditions.
Quantum chaos theory studies how the correspondence between quantum mechanics and classical mechanics works in the context of chaotic systems. Relativistic chaos describes chaotic systems under general relativity.
The motion of a system of three or more stars interacting gravitationally (the gravitational N-body problem) is generically chaotic.
In electrical engineering, chaotic systems are used in communications, random number generators, and encryption systems.
In numerical analysis, the Newton-Raphson method of approximating the roots of a function can lead to chaotic iterations if the function has no real roots.
The Butterfly Effect is a phrase that encapsulates the more technical notion of sensitive dependence on initial conditions in chaos theory. The idea is that small variations in the initial conditions of a dynamical system produce large variations in the long term behavior of the system. Sensitive dependence is also found in non-dynamical systems: for example, a ball placed at the crest of a hill might roll into any of several valleys depending on slight differences in initial position.
The practical consequence of the butterfly effect is that complex systems such as the weather are difficult to predict past a certain time range - approximately a week, in the case of weather. This is because any finite model that attempts to simulate a system must necessarily truncate some information about the initial conditions - for example, when simulating the weather, one would not be able to include the wind coming from every butterfly's wings. In all practical cases, defects in the knowledge of the initial conditions and deficiencies in the model are equally important sources of error. In a chaotic system, these errors are magnified as the simulation progresses. Thus the predictions of the simulation are useless after a certain finite amount of time.
Edward Lorenz first analyzed the effect in a 1963 paper for the New York Academy of Sciences. According to the paper, "One meteorologist remarked that if the theory were correct, one flap of a seagull's wings could change the course of weather forever." Later speeches and papers by Lorenz used the more poetic butterfly, possibly inspired by the diagram generated by the Lorenz attractor, which looks like a butterfly; other theories propose that the phrase's basis is to be found in fiction (Ray Bradbury's 1952 story "A Sound of Thunder"), but there is no proof available that Lorenz was swayed by literary precedent. The idea is now often stated something to the effect of, "a butterfly flapping its wings in Tokyo could cause tornadoes in California."
The concept of the Butterfly effect is sometimes used in popular media dealing with the idea of time travel, though not always accurately. For example, in the movie A Sound of Thunder the characters are determined not to change anything in the past - but in reality their mere presence could be enough to change short-term events (such as the weather), and could also have an unpredictable impact on the distant future.
In many cases, minor and seemingly inconsequential actions in the past are extrapolated over time and can have radical effects on the present time of the main characters. In the movie The Butterfly Effect, Evan Treborn (Ashton Kutcher), when reading from his adolescent journals, is able to essentially "redo" parts of his past. As he continues to do this, he realizes that even though his intentions are good, the actions he takes always have unintended consequences.
Theories abound as to real-life examples of this phenomenon:
The stock market: slight fluctuations in one market can effect many others.
Biology: A small change in a virus in monkeys in Africa creates a "thunderstorm" of an effect on the human population around the world with the appearance of the AIDs virus.
Evolution: small changes in the chemistry of the early Earth gives rise to life.
Psychology: Thought patterns and consciousness altered by small changes in brain chemistry or small changes in physical environmental stimuli.
The butterfly effect occurs under two conditions:
Each state of the system is determined by the previous state. In other words, the output at each moment is repeatedly entered back into the system for another cycle through the mathematical functions that determine the system.
The result of the butterfly effect is unpredictability. Small differences in initial input can have dramatically different results after several cycles through the system. In the fractals pictured above, points that are very close together can be different colors. The results can tend toward infinity at different rates or toward zero, even though the initial points are very close together.
�In mathematics and physics, chaos theory deals with the behavior of certain nonlinear dynamic systems that under certain conditions exhibit a phenomenon known as chaos, which is characterized by a sensitivity to initial conditions (see butterfly effect). As a result of this sensitivity, the behavior of systems that exhibit chaos appears to be random, even though the model of the system is deterministic in the sense that it is well defined and contains no random parameters. Examples of such systems include the atmosphere, the solar system, plate tectonics, turbulent fluids, economies, and population growth.
Systems that exhibit mathematical chaos are deterministic and thus orderly in some sense; this technical use of the word chaos is at odds with common parlance, which suggests complete disorder. See the article on mythological chaos for a discussion of the origin of the word in mythology, and other uses. Chaos theory deals with deterministic systems, and a related field of physics called quantum chaos theory studies non-deterministic systems that follow the laws of quantum mechanics.
A non-linear dynamical system can exhibit one or more of the following types of behavior:
forever expanding (only for unbounded systems)
periodic motion
quasi-periodic motion
chaotic motion
The type of behavior a system may exhibit depends on the initial state of the system and the values of its parameters, if any. The most difficult type of behavior to characterize and predict is chaotic motion, a non-periodic complex motion, for which the theory is named.
For a system to be classified as chaotic, it must have the following properties:
it must be sensitive to initial conditions
it must be topologically mixing
its periodic orbits must be dense
Sensitivity to initial conditions means that two points in such a system may move in vastly different trajectories in their phase space, even if the difference in their initial configurations is very small. The systems behave identically only if their initial configurations are exactly the same. An example of such sensitivity is the so-called "butterfly effect", which suggests that the flapping of a butterfly's wings might create tiny changes in the atmosphere, which could over time cause a tornado to occur. The flapping wing represents a small change in the initial condition of the system, which causes a chain of events leading to large-scale phenomena. Had the butterfly not flapped its wings, the trajectory of the system might have been vastly different.
Topologically mixing means that system will evolve over time so that any given region or open set of its phase space will eventually overlap with any other given region. Since phase space is of finite size, this usually means that the phase space will become thoroughly mixed together after a fairly short time. Here, "mixing" is really meant to correspond to the standard intuition: the mixing of colored dyes or fluids is an example of a chaotic system.
One way of visualizing chaotic motion, or indeed any type of motion, is to make a phase diagram of the motion. In such a diagram time is implicit and each axis represents one dimension of the state. For instance, one might plot the position of a pendulum against its velocity. A pendulum at rest will be plotted as a point and a one in periodic motion will be plotted as a simple closed curve. When such a plot forms a closed curve, the curve is called an orbit. Our pendulum has an infinite number of such orbits, forming a pencil of nested ellipses about the origin.
Often phase diagrams reveal that most state trajectories wind up approaching some common limit. The system ends up doing the same motion for all initial states in a region around the motion, almost as though the system is attracted to that motion. Such attractive motion is fittingly called an attractor for the system and is very common for forced dissipative systems.
For instance, if we attach a damper to our pendulum, no matter what its initial position and velocity it will wind up being at rest - or more correctly: it will reach rest at the limit. The trajectories on the phase diagram will all spiral in towards the middle, rather than forming sets of ovals. This point in the middle - the state when the pendulum is at rest - is called an "attractor". Attractors are often associated with dissipative systems like this, where some element (the damper) dissipates energy.
Such an attractor may be called a "point attractor". Not all attractors are points. Some are simple loops, or more complex doubled loops (for which you need more than two degrees of freedom). And some are actually fractals: the so called "strange attractors". Systems with loop attractors exhibit periodic motion. Those with more complex split loops tend to exhibit quasiperiodic motion. And systems with strange attractors tend to exhibit chaotic behavior.
At any point on the phase diagram, the system will tend to evolve to another neighboring state in some sort of deterministic way. If our pendulum is at a particular position and traveling with a particular velocity, we can calculate what its (infinitesimally) "next" position and velocity will be. That is, we can treat our phase diagram as being a vector field, and use vector calculus to understand it. Attractors in our phase diagram are simply those regions with a negative divergence.
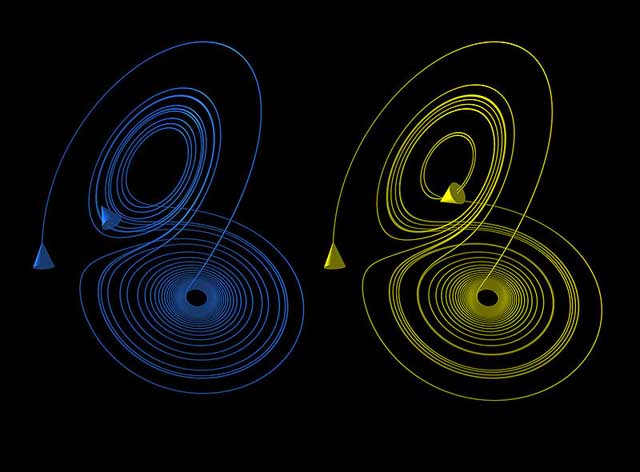
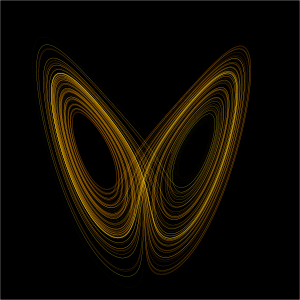
While most of the motion types mentioned above give rise to very simple attractors, such as points and circle-like curves called limit cycles, chaotic motion gives rise to what are known as strange attractors, attractors that can have great detail and complexity. For instance, a simple three-dimensional model of the Lorenz weather system gives rise to the famous Lorenz attractor. The Lorenz attractor is perhaps one of the best-known chaotic system diagrams, probably because not only was it one of the first, but it is one of the most complex and as such gives rise to a very interesting pattern which looks like the wings of a butterfly. Another such attractor is the Rossler Map, which experiences period-two doubling route to chaos, like the logistic map.
Strange attractors occur in both continuous dynamical systems (such as the Lorenz system) and in some discrete systems (such as the Henon map). Other discrete dynamical systems have a repelling structure called a Julia set which forms at the boundary between basins of attraction of fixed points - Julia sets can be thought of as strange repellers. Both strange attractors and Julia sets typically have a fractal structure.
The Poincare-Bendixson theorem shows that a strange attractor can only arise in a continuous dynamical system if it has three or more dimensions. However, no such restriction applies to discrete systems, which can exhibit strange attractors in two or even one dimensional systems.
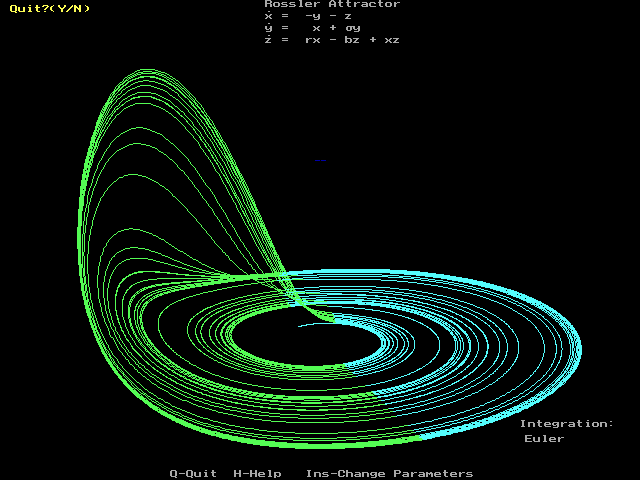
Click to see animated versions.
To his surprise the weather that the machine began to predict was completely different to the weather calculated before. Lorenz tracked this down to the computer printout. The printout rounded variables off to a 3-digit number, but the computer worked with 6-digit numbers. This difference is tiny and the consensus at the time would have been that it should have had practically no effect. However Lorenz had discovered that small changes in initial conditions produced large changes in the long-term outcome.The term chaos as used in mathematics was coined by the applied mathematician James A. Yorke. Read more ...

Chaos Mythology
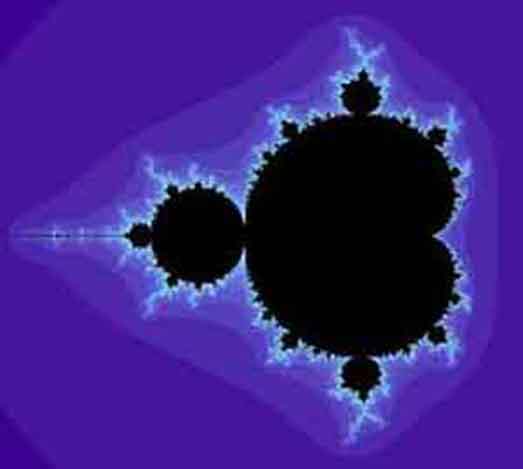
Fractals