

Quantum mechanics (QM; also known as quantum physics, or quantum theory) is a fundamental branch of physics which deals with physical phenomena at nanoscopic scales, where the action is on the order of the Planck constant. The name derives from the observation that some physical quantities can change only in discrete amounts (Latin quanta), and not in a continuous (cf. analog) way. It departs from classical mechanics primarily at the quantum realm of atomic and subatomic length scales.
Quantum mechanics provides a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. Quantum mechanics provides a substantially useful framework for many features of the modern periodic table of elements, including the behavior of atoms during chemical bonding, and has played a significant role in the development of many modern technologies.
The earliest versions of quantum mechanics were formulated in the first decade of the 20th century. About this time, the atomic theory and the corpuscular theory of light (as updated by Einstein) first came to be widely accepted as scientific fact; these latter theories can be viewed as quantum theories of matter and electromagnetic radiation, respectively.
Early quantum theory was significantly reformulated in the mid-1920s by Werner Heisenberg, Max Born and Pascual Jordan (matrix mechanics); Louis de Broglie and Erwin Schrodinger (wave mechanics); and Wolfgang Pauli and Satyendra Nath Bose (statistics of subatomic particles). Moreover, the Copenhagen interpretation of Niels Bohr became widely accepted. By 1930, quantum mechanics had been further unified and formalized by the work of David Hilbert, Paul Dirac and John von Neumann with a greater emphasis placed on measurement in quantum mechanics, the statistical nature of our knowledge of reality, and philosophical speculation about the role of the observer.
Quantum mechanics has since permeated throughout many aspects of 20th-century physics and other disciplines including quantum chemistry, quantum electronics, quantum optics, and quantum information science. Much 19th-century physics has been re-evaluated as the "classical limit" of quantum mechanics and its more advanced developments in terms of quantum field theory, string theory, and speculative quantum gravity theories. Read More
Caltech's massive 6,100-qubit array brings the quantum future closer Science Daily - September 25, 2025

Caltech scientists have built a record-breaking array of 6,100 neutral-atom qubits, a critical step toward powerful error-corrected quantum computers. The qubits maintained long-lasting superposition and exceptional accuracy, even while being moved within the array. This balance of scale and stability points toward the next milestone: linking qubits through entanglement to unlock true quantum computation.
Explaining a quantum oddity with five atoms PhysOrg - September 2, 2025 Science Daily - September 2, 2025

Matter gets weird at the quantum scale, and among the oddities is the Efimov effect, a state in which the attractive forces between three or more atoms bind them together, even as they are excited to higher energy levels, while that same force is insufficient to bind two atoms.
Strange' heavy' electrons could be the future of quantum computing

Discovery of Planckian time limit opens doors to novel quantum technologies.
Probability theorem gets quantum makeover after 250 years PhysOrg - August 31, 2025

How likely you think something is to happen depends on what you already believe about the circumstances. That is the simple concept behind Bayes' rule, an approach to calculating probabilities, first proposed in 1763. Now, an international team of researchers has shown how Bayes' rule operates in the quantum world
Researchers discover universal rules of quantum entanglement across all dimensions PhysOrg - August 7, 2025

A team of theoretical researchers used thermal effective theory to demonstrate that quantum entanglement follows universal rules across all dimensions.
Scientists Just Admitted Nobody Really Gets Quantum Physics Science Alert - August 3, 2025

The theory of quantum mechanics has transformed daily life since being proposed a century ago, yet how it works remains a mystery Š and physicists are deeply divided about what is actually going on
Quantum Teleportation Achieved Over Internet For The First Time Science Alert - March 28, 2025

A quantum state of light was successfully teleported through more than 30 kilometers (around 18 miles) of fiber optic cable amid a torrent of internet traffic - a feat of engineering once considered impossible.
Quantum Experiment Reveals Light Existing in Dozens of Dimensions Science Alert - February 3, 2025

A paradox at the heart of quantum physics has been tested in an extraordinary fashion, pushing the boundaries of human intuition beyond breaking point by measuring a pulse of light in 37 dimensions.
Physicists Measure Quantum Geometry of Electrons For First Time Science Alert - January 5, 2025

A new breakthrough may help scientists solve some of the mysteries of the quantum realm. For the first time, physicists have been able to measure the geometrical 'shape' a lone electron adopts as it moves through a solid. It's an achievement that will unlock a whole new way of studying how crystalline solids behave on a quantum level.
Physicists Discover 'Quantum Embezzlement' Could Offer Infinite Source of Entanglement Science Alert - December 30, 2024

Knowing infinite levels of entanglement could naturally be occurring in absolute nothingness could point the way to a whole 'criminal underworld' of physics, where different classes of theft occur right under our noses.
Can entangled particles communicate faster than light? PhysOrg - December 25, 2024

Entanglement is perhaps one of the most confusing aspects of quantum mechanics. On its surface, entanglement allows particles to communicate over vast distances instantly, apparently violating the speed of light. But while entangled particles are connected, they don't necessarily share information between them.
Team presents first demonstration of quantum teleportation over busy internet cables PhysOrg - December 20, 2024

The discovery introduces the new possibility of combining quantum communication with existing internet cables - greatly simplifying the infrastructure required for distributed quantum sensing or computing applications.
Atoms squished closer together than ever before, revealing seemingly impossible quantum effects Live Science - May 15, 2024
Scientists have squished two layers of ultracold magnetic atoms to within 50 nanometers of each other - 10 times closer than in previous experiments - revealing bizarre quantum effects not seen before.
For The First Time, Physicists 'Entangle' Individual Molecules With Staggering Precision

Bulky and hard to wrangle, molecules have long defied physicists' attempts to lure them into a state of controlled quantum entanglement, whereby the molecules are intimately linked even at a distance. Now, for the first time, two separate teams have succeeded in entangling pairs of ultra-cold molecules using the same method: microscopically precise optical 'tweezer traps'.
Highest-Energy Detection Of Quantum Entanglement Achieved Yet IFL Science - September 29, 2023

CERNÕs ATLAS experiment has measured the quantum entanglement of top quarks, the most massive fundamental particles, at the highest energy yet, 12 orders of magnitudes (one trillion times) higher than standard entanglement experiments. Quantum entanglement is a property that we do not experience at our level of reality. It is very much in the domain of the smallest players in the universe. When particles are entangled, they can only be understood as part of a single state and not as individuals anymore. So if something affects one, the other will be instantaneously affected, even if it was on the other side of the universe. This might seem a violation of special relativity and the finiteness of the speed of light but it isnÕt, although Einstein was very bothered by it and called it 'spooky action at a distance.'
'Spooky action at a distance' can lead to a multiverse. Here's how. Space.com - October 24, 2022
Some interpretations of quantum mechanics propose that our entire universe is described by a single universal wave function that constantly splits and multiplies, producing a new reality for every possible quantum interaction. That's quite a bold statement. So how do we get there? One of the earliest realizations in the history of quantum mechanics is that matter has a wave-like property. The first to propose this was French physicist Louis de Broglie, who argued that every subatomic particle has a wave associated with it, just like light can behave like both a particle and a wave.
A Surprising Number of Genetic Mutations Occur Thanks to a Quirk of Quantum Physics Science Alert - May 7, 2022

Mistakes happen. Especially when it comes to the replication of vast sequences of DNA inside our cells. It's a good thing too. If not for the errors in our genes we refer to as mutations, natural selection would be a no-go, and life would be dead in the water.
Quantum mechanics could explain why DNA can spontaneously mutate PhysOrg - May 7, 2022
The molecules of life, DNA, replicate with astounding precision, yet this process is not immune to mistakes and can lead to mutations. Using sophisticated computer modeling, a team of physicists and chemists have shown that such errors in copying can arise due to the strange rules of the quantum world.
Imaginary numbers could be needed to describe reality, new studies find Live Science - December 21, 2021

Imaginary numbers are what you get when you take the square root of a negative number, and they have long been used in the most important equations of quantum mechanics, the branch of physics that describes the world of the very small. When you add imaginary numbers and real numbers, the two form complex numbers, which enable physicists to write out quantum equations in simple terms. But whether quantum theory needs these mathematical chimeras or just uses them as convenient shortcuts has long been controversial. In fact, even the founders of quantum mechanics themselves thought that the implications of having complex numbers in their equations was disquieting. In a letter to his friend Hendrik Lorentz, physicist Erwin Schrdinger - the first person to introduce complex numbers into quantum theory, with his quantum wave function ...
Harvard-MIT Quantum Computing Breakthrough - We Are Entering a Completely New Part of the Quantum World SciTech Daily - July 10, 2021
Quantum entanglement realized between distant large objects PhysOrg - September 28, 2020

Entanglement is the basis for quantum communication and quantum sensing. It can be understood as a quantum link between two objects which makes them behave as a single quantum object. Researchers succeeded in making entanglement between a mechanical oscillator - a vibrating dielectric membrane - and a cloud of atoms, each acting as a tiny magnet, or what physicists call "spin." These very different entities were possible to entangle by connecting them with photons, particles of light. Atoms can be useful in processing quantum information and the membrane - or mechanical quantum systems in general - can be useful for storage of quantum information
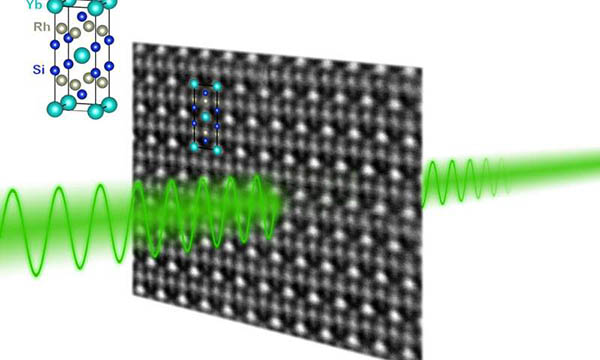
Billions of quantum entangled electrons found in 'strange metal' PhysOrg - January 16, 2020
In a new study, U.S. and Austrian physicists have observed quantum entanglement among "billions of billions" of flowing electrons in a quantum critical material. The research examined the electronic and magnetic behavior of a "strange metal" compound of ytterbium, rhodium and silicon as it both neared and passed through a critical transition at the boundary between two well-studied quantum phases.
2,000 Atoms Exist in Two Places at Once in Unprecedented Quantum Experiment PhysOrg - October 4, 2019
The new experiment demonstrated a bizarre quantum effect from the double-slit experiment at an unprecedented scale. Giant molecules can be in two places at once, thanks to quantum physics. That's something that scientists have long known is theoretically true based on a few facts: Every particle or group of particles in the universe is also a wave - even large particles, even bacteria, even human beings, even planets and stars. And waves occupy multiple places in space at once. So any chunk of matter can also occupy two places at once. Physicists call this phenomenon "quantum superposition," and for decades, they have demonstrated it using small particles
Quantum gravity's tangled time PhysOrg - August 25, 2019
The theories of quantum mechanics and gravity are notorious for being incompatible, despite the efforts of scores of physicists over the past fifty years. However, recently an international team of researchers have combined the key elements of the two theories describing the flow of time and discovered that temporal order between events can exhibit genuine quantum features.
Cracking a decades-old test, researchers bolster case for quantum mechanics PhysOrg - August 22, 2019
Scientists unveil the first-ever image of quantum entanglement PhysOrg - July 14, 2019
For the first time ever, physicists have managed to take a photo of a strong form of quantum entanglement called Bell entanglement - capturing visual evidence of an elusive phenomenon which a baffled Albert Einstein once called 'spooky action at a distance'.
Quantum physicists achieve entanglement record PhysOrg - April 16, 2018
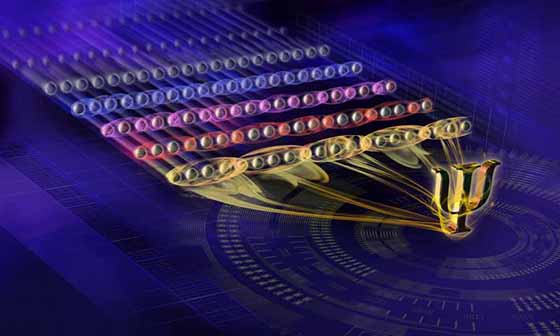
Physically, entangled particles cannot be described as individual particles with defined states, but only as a complete system. It is particularly difficult to understand entanglement when numerous particles are involved. Here, a distinction must be made between the entanglement of individual particles and genuine multi-particle entanglement. This can only be understood as a property of the overall system of all particles concerned, and cannot be explained by a combination of the subsystems being entangled.
Massive astrophysical objects governed by subatomic equation PhysOrg - March 5, 2018
Quantum mechanics is the branch of physics governing the sometimes-strange behavior of the tiny particles that make up our universe. Equations describing the quantum world are generally confined to the subatomic realm - the mathematics relevant at very small scales is not relevant at larger scales, and vice versa. However, a surprising new discovery from a Caltech researcher suggests that the Schrodinger Equation - the fundamental equation of quantum mechanics - is remarkably useful in describing the long-term evolution of certain astronomical structures. Massive astronomical objects are frequently encircled by groups of smaller objects that revolve around them, like the planets around the sun. For example, supermassive black holes are orbited by swarms of stars, which are themselves orbited by enormous amounts of rock, ice, and other space debris. Due to gravitational forces, these huge volumes of material form into flat, round disks. These disks, made up of countless individual particles orbiting en masse, can range from the size of the solar system to many light-years across.
4D World: Light Moving In Fourth Dimension Observed During Quantum Hall Experiment IBTimes - January 9, 2018
Two experiments used different methods in a two-dimensional space to simulate a four-dimensional one. In one setup, the scientists used lasers to create 2D pathways through glass and then sent lightwaves through. In another, they used crisscrossed laser beams to influence the motion of super cold atoms. With both of the systems, they were seemingly forcing the materials inside to move within another dimension, a simulated one. Although they could not physically see that dimension they were building, the scientists observed the material sent through their experiments to find evidence of the fourth-dimensional quantum Hall effect. Quantum Hall Effect
Breaking the rules: Heavy chemical elements alter theory of quantum mechanics PhysOrg - October 3, 2017
A series of complicated experiments involving one of the least understood elements of the Periodic Table has turned some long-held tenets of the scientific world upside down. Researchers found that the theory of quantum mechanics does not adequately explain how the heaviest and rarest elements found at the end of the table function. Instead, another well-known scientific theory - Albert Einstein's famous Theory of Relativity helps govern the behavior of the last 21 elements of the Periodic Table.
'Angel particle' which is both matter and anti-matter is discovered after an 80-year quest in a 'landmark' breakthrough for quantum physics Daily Mail - July 21, 2017
Researchers revealed that they have found the first evidence of the elusive particles in what is being described as a 'landmark' moment in quantum physics. The discovery could help scientists to bring a quantum computing revolution, which would allow us to make machines many times more powerful than those made using existing technology.Scientists have theorized that when the Big Bang first created the universe, equal amounts of matter and anti-matter were produced. Anti-matter is made from particles which are the 'anti-particles' of those from normal matter.
Here's How Scientists Teleported the First Object Into Space Seeker - July 13, 2017
Chinese researchers successfully realized ground-to-satellite quantum teleportation using a photon particle - a feat that could one day make for a better and more secure internet. Scientists from China have just performed the first ever quantum teleportation from Earth to space. Does this mean we are now living in the future envisioned in Star Trek? Actually, no physical matter was actually Ņbeamed up,Ó unfortunately - just photons. But this breakthrough might make for a better and more secure internet in the future. "Quantum teleportation brings to mind Star TrekÕs transporter, where crew members are disassembled in one location to be reassembled in another. Real quantum teleportation is a much more subtle effect where information is transferred between entangled quantum states. ItÕs a quantum trick that could give us the ultimate in secure communication.
Weird quantum effects stretch across hundreds of miles Science Daily - July 19, 2016
Scientists have discovered strange quantum effects hold, even over hundreds of miles. In longest test of quantum mechanics, researchers find neutrinos, traveling over 450 miles at close to speed of light, have no single identity. In the world of quantum, infinitesimally small particles, weird and often logic-defying behaviors abound. Perhaps the strangest of these is the idea of superposition, in which objects can exist simultaneously in two or more seemingly counterintuitive states. For example, according to the laws of quantum mechanics, electrons may spin both clockwise and counter-clockwise, or be both at rest and excited, at the same time.
Quantum Computer Could Simulate Beginnings of the Universe Live Science - June 27, 2016
Quantum mechanics suggest that seemingly empty space is actually filled with ghostly particles that are fluctuating in and out of existence. And now, scientists have for the first time made an advanced machine known as a quantum computer simulate these so-called virtual particles. This research could help shed light on currently hidden aspects of the universe, from the hearts of neutron stars to the very first moments of the universe after the Big Bang, researchers said. Quantum mechanics suggests that the universe is a fuzzy, surreal place at its smallest levels. For instance, atoms and other particles can exist in states of flux known as superpositions, where they can seemingly each spin in opposite directions simultaneously, and they can also get entangled - meaning they can influence each other instantaneously no matter how far apart they are separated. Quantum mechanics also suggests that pairs of virtual particles, each consisting of a particle and its antiparticle, can wink in and out of seemingly empty vacuum and influence their surroundings.
Entanglement for identical particles doesn't follow textbook rules PhysOrg - February 9, 2016
In quantum entanglement, two particles are correlated in such a way that any action on one of them affects the other even when they are far apart. The traditional methods of measuring the degree of quantum entanglement were originally developed for nonidentical particles, such as between an electron and a proton, or two atoms of different types. Unfortunately, these methods do not work very well when applied to identical particles, such as two electrons or two helium atoms, since such particles are indistinguishable. The traditional methods often give false positives for entanglement between identical particles, claiming that they are entangled even when it's clear that they are not.
New method of quantum entanglement vastly increases how much information can be carried in a photon PhysOrg - June 30, 2015
A team of researchers has demonstrated a new way to harness light particles, or photons, that are connected to each other and act in unison no matter how far apart they are - a phenomenon known as quantum entanglement. In previous studies, photons have typically been entangled by one dimension of their quantum properties - usually the direction of their polarization. In the new study, researchers demonstrated that they could slice up and entangle each photon pair into multiple dimensions using quantum properties such as the photons' energy and spin. This method, called hyperentanglement, allows each photon pair to carry much more data than was possible with previous methods.
Quantum Cheshire Cat effect may be explained by standard quantum mechanics PhysOrg - June 13, 2015
"A grin without a cat" is how Lewis Carroll describes the Cheshire Cat's mysterious way of disappearing while leaving its grin behind in his 1865 classic, Alice in Wonderland. The fanciful character raises a question that has captured physicists' attention over the past few years: can an object be separated from its properties? However, in a new paper published in the New Journal of Physics has questioned this interpretation of the results. Instead of a particle being separated from its properties, they suggest that the results can be explained by a standard quantum effect, quantum interference, in which an individual particle interferes with itself due to its wave-like properties.
Strange behavior of quantum particles may indicate the existence of other parallel universes PhysOrg - June 6, 2015
Quantum mechanics is a strange realm of reality. Particles at this atomic and subatomic level can appear to be in two places at once. Because the activity of these particles is so iffy, scientists can only describe what's happening mathematically by "drawing" the tiny landscape as a wave of probability.
Game theory elucidates the collective behavior of bosons PhysOrg - April 28, 2015
When scientists explore the mysterious behavior of quantum particles, they soon reach the limits of present-day experimental research. There are two kinds of quantum particles in nature: fermions and bosons. Whether a particle is a fermion or a boson depends on its intrinsic angular momentum or spin. For fermions, the spin is always half-integer valued and the most prominent example is the electron. Bosons, on the other hand, always exhibit integer spins. Such is the case for photons, for example, but also whole atoms may be bosons. Bosons are social beasts that like to be on the same wavelength Š or, as physicists put it, they like to be in the same quantum state.
The beginning of everything: A new paradigm shift for the infant universe PhysOrg - November 29, 2012
A new paradigm for understanding the earliest eras in the history of the universe has been developed by scientists at Penn State University. Using techniques from an area of modern physics called loop quantum cosmology, the scientists now have extended analyses that include quantum physics farther back in time than ever before - all the way to the beginning. The new paradigm of loop quantum origins shows, for the first time, that the large-scale structures we now see in the universe evolved from fundamental fluctuations in the essential quantum nature of "space-time," which existed even at the very beginning of the universe over 14 billion years ago. The achievement also provides new opportunities for testing competing theories of modern cosmology against breakthrough observations expected from next-generation telescopes.
Quantum test pricks uncertainty BBC - September 8, 2012

Pioneering experiments have cast doubt on a founding idea of the branch of physics called quantum mechanics. The Heisenberg uncertainty principle is in part an embodiment of the idea that in the quantum world, the mere act of observing an event changes it. But the idea had never been put to the test, and a team writing in Physical Review Letters says "weak measurements" prove the rule was never quite right. That could play havoc with "uncrackable codes" of quantum cryptography. Quantum mechanics has since its very inception raised a great many philosophical and metaphysical debates about the nature of nature itself.
Quantum Entanglement Holds DNA Together, Say Physicists Technology Review - January 11, 2012
A new theoretical model suggests that quantum entanglement helps prevent the molecules of life from breaking apart. There was a time, not so long ago, when biologists swore black and blue that quantum mechanics could play no role in the hot, wet systems of life. Since then, the discipline of quantum biology has emerged as one of the most exciting new fields in science
Vibration rocks for entangled diamonds PhysOrg - December 16, 2011
You can take two diamonds - not quite everyday objects, but at least simple and recognizable - and put them in such a state: in particular a superposition of a state of one diamond vibrating and the other not, and vice versa.
Two Diamonds Linked by Strange Quantum Entanglement Live Science - December 1, 2011
Scientists have linked two diamonds in a mysterious process called entanglement that is normally only seen on the quantum scale. Entanglement is so weird that Einstein dubbed it "spooky action at a distance." It's a strange effect where one object gets connected to another so that even if they are separated by large distances, an action performed on one will affect the other. Entanglement usually occurs with subatomic particles, and was predicted by the theory of quantum mechanics, which governs the realm of the very small. But now physicists have succeeded in entangling two macroscopic diamonds, demonstrating that quantum mechanical effects are not limited to the microscopic scale.
One clock with two times: When quantum mechanics meets general relativity PhysOrg - October 20, 2011
>
According to general relativity, time flows differently at different positions due to the distortion of space-time by a nearby massive object. A single clock being in a superposition of two locations allows probing quantum interference effects in combination with general relativity.
Near-Perfect Particle Measurement Achieved Live Science - July 14, 2011
The mind-bending laws of quantum mechanics say we can't observe the smallest particles without affecting them. Physicists have now caused the smallest-ever disturbance while making a quantum measurement - in fact, almost the minimum thought to be possible. This disturbance is called back-action, and it is one of the hallmarks of quantum mechanics, which governs the actions of the very small. It arises from the supposition that before a measurement is made, particles exist in a sort of limbo state, being neither here nor there while retaining the possibility of either.
Bridging the gap to quantum world BBC - June 3, 2009
Scientists have "entangled" the motions of pairs of atoms for the first time.
Entanglement is an effect in quantum mechanics, a relatively new branch of physics that is based more in probability than in classical laws. It describes how properties of two or more objects can be inextricably linked over "vast" distances. The results, published in Nature, further bridge the gap between the world of quantum mechanics and the laws of everyday experience.
This is the first time entanglement has been seen in a so-called "mechanical system". The phenomenon suggests that a measurement performed on one object can affect the measurement on another object some distance away.
Einstein's 'Spooky Physics' Gets More Entangled Live Science - June 3, 2009
Quantum entanglement is just spooky - even Einstein thought so. As if particles (as in particle physics) have telepathic empathy. The theory of quantum mechanics predicts that two or more particles can become "entangled" so that even after they are separated in space, when an action is performed on one particle, the other particle responds immediately. Scientists still don't know how the particles send these instantaneous messages to each other, but somehow, once they are entwined, they retain a fundamental connection. This bizarre idea riled Einstein so much he called it "spooky action at a distance."