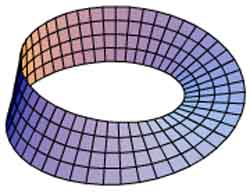
In mathematics, a Mobius strip, Mobius band, or Mobius loop[a] is a surface that can be formed by attaching the ends of a strip of paper together with a half-twist. As a mathematical object, it was discovered by Johann Benedict Listing and August Ferdinand Mobius in 1858, but it had already appeared in Roman mosaics from the third century CE.

The Mobius strip is a non-orientable surface, meaning that within it one cannot consistently distinguish clockwise from counterclockwise turns. Every non-orientable surface contains a Mobius strip.

As an abstract topological space, the Mobius strip can be embedded into three-dimensional Euclidean space in many different ways: a clockwise half-twist is different from a counterclockwise half-twist, and it can also be embedded with odd numbers of twists greater than one, or with a knotted centerline.

Any two embeddings with the same knot for the centerline and the same number and direction of twists are topologically equivalent. All of these embeddings have only one side, but when embedded in other spaces, the Mobius strip may have two sides. It has only a single boundary curve.

Several geometric constructions of the Mobius strip provide it with additional structure. It can be swept as a ruled surface by a line segment rotating in a rotating plane, with or without self-crossings. A thin paper strip with its ends joined to form a Mobius strip can bend smoothly as a developable surface or be folded flat; the flattened Mobius strips include the trihexaflexagon.

The Sudanese Mobius strip is a minimal surface in a hypersphere, and the Meeks Mobius strip is a self-intersecting minimal surface in ordinary Euclidean space. Both the Sudanese Mobius strip and another self-intersecting Mobius strip, the cross-cap, have a circular boundary.

A Mobius strip without its boundary, called an open Mobius strip, can form surfaces of constant curvature. Certain highly-symmetric spaces whose points represent lines in the plane have the shape of a Mobius strip.

The many applications of Mobius strips include mechanical belts that wear evenly on both sides, dual-track roller coasters whose carriages alternate between the two tracks, and world maps printed so that antipodes appear opposite each other.

Mobius strips appear in molecules and devices with novel electrical and electromechanical properties, and have been used to prove impossibility results in social choice theory.

In popular culture, Mobius strips appear in artworks by M. C. Escher, Max Bill, and others, and in the design of the recycling symbol. Many architectural concepts have been inspired by the Mobius strip, including the building design for the NASCAR Hall of Fame.

Performers including Harry Blackstone Sr. and Thomas Nelson Downs have based stage magic tricks on the properties of the Mobius strip. The canons of J. S. Bach have been analyzed using Mobius strips. Many works of speculative fiction feature Mobius strips; more generally, a plot structure based on the Mobius strip, of events that repeat with a twist, is common in fiction. Continue reading

There have been technical applications. Giant Mobius strips have been used as conveyor belts that last longer because the entire surface area of the belt gets the same amount of wear, and as continuous-loop recording tapes (to double the playing time). Mobius strips are common in the manufacture of fabric computer printer and typewriter ribbons, as they allow the ribbon to be twice as wide as the print head whilst using both half-edges evenly.

There have been several technical applications for the Mobius strip. Giant Mobius strips have been used as conveyor belts that last longer because the entire surface area of the belt gets the same amount of wear, and as continuous-loop recording tapes (to double the playing time). Mobius strips are common in the manufacture of fabric computer printer and typewriter ribbons, as they allow the ribbon to be twice as wide as the print head while using both half-edges evenly.

A device called a Mobius resistor is an electronic circuit element which has the property of canceling its own inductive reactance. Nikola Tesla patented similar technology in the early 1900s: "Coil for Electro Magnets" was intended for use with his system of global transmission of electricity without wires.

The international symbol for recycling is a Mobius loop.

The Mobius strip has provided inspiration both for sculptures and for graphical art. The artist M. C. Escher was especially fond of it and based several of his lithographs on it. One famous example, Mobius Strip II, features ants crawling around the surface of a Mobius strip.

It is also a recurrent feature in science fiction stories, such as Arthur C. Clarke's The Wall of Darkness.

Science fiction stories sometimes suggest that our universe might be some kind of generalized Mobius strip. In the short story "A Subway Named Mobius", by A.J. Deutsch, the Boston subway authority builds a new line, but the system becomes so tangled that it turns into a Mobius strip, and trains start to disappear. The Mobius strip also features prominently in Brian Lumley's Necroscope series of novels.

Medals, such as those awarded in competitions like the Olympics, often feature a neck ribbon configured as a Mobius strip. This allows the ribbon to fit comfortably around the neck while the medal lies flat on the chest.

The Mobius strip is the configuration space of two unordered points on a circle. Consequently, in music theory, the space of all two note chords, known as dyads, takes the shape of a Mobius strip; this and generalizations to more points is a significant application of orbifolds to music theory. Read more

Mobius Mystery Solved By Mathematician After 5 Decades   IFL Science - October 16, 2023

Mobius strips are fun geometrical shapes that only have one side. Take a strip of paper - it's got a front and a back. Now twist it and glue the two short edges together. Suddenly there is no front or back. You could draw a line across its whole surface without having to lift the pencil from the paper. Forty-six years ago mathematicians suggested the minimum size for such a strip but they couldn't prove it. Now, someone finally has.

Mathematicians Solve A Key Mobius Strip Problem, After Almost 50 Years of Searching   Science Alert - September 13, 2023

For nearly fifty years, mathematicians have puzzled over a deceptively simple question: how small can you make a Mobius strip without it intersecting itself?

The weird world of one-sided objects   PhysOrg - September 24, 2018

You have most likely encountered one-sided objects hundreds of times in your daily life - like the universal symbol for recycling, found printed on the backs of aluminum cans and plastic bottles. A Mobius strip can be created by taking a strip of paper, giving it an odd number of half-twists, then taping the ends back together to form a loop. If you take a pencil and draw a line along the center of the strip, you'll see that the line apparently runs along both sides of the loop. The concept of a one-sided object inspired artists like Dutch graphic designer M.C. Escher, whose woodcut "Mobius Strip II" shows red ants crawling one after another along a Mobius strip.