
Mathematics in China emerged independently by the 11th century BC. The Chinese independently developed very large and negative numbers, decimals, a decimal system, a binary system, algebra, geometry, trigonometry.
Most scholars believe that Chinese mathematics and the mathematics of the ancient Mediterranean world had developed more or less independently up to the time when the The Nine Chapters on the Mathematical Art reached its final form, while the Writings on Reckoning and Huainanzi preceded it. It is often suggested that some Chinese mathematical discoveries predate their Western counterparts. One example is the Pythagorean theorem. There is some controversy regarding this issue and the precise nature of this knowledge in early China. The Chinese were one of the most advanced in dealing with mathematical computations, and created enormous numbers. Elements of "Pythagorean" science have been found, for example, in one of the oldest Classical Chinese texts (see King Wen sequence). This book was known for all of the mathematical information it contained. Knowledge of Pascal's triangle has also been shown to have existed in China centuries before Pascal, such as by Shen Kuo.
Knowledge of Chinese mathematics before 100 BC is somewhat fragmentary, and even after this date the manuscript traditions are obscure. The dating of the use of certain mathematical methods in Chinese history is problematic and disputed.
In early times the focus was on astronomy and perfecting the calendar and not on establishing the proof. Many works simply listed equations or gave diagrams where a proof was hinted at rather than shown. In other cases a proof was shown but it was declared to be an established method after some fashion.
Simple mathematics inscribed on tortoise shells for writing mediums date back to the Shang Dynasty (1600 BC-1050 BC). One of the oldest surviving mathematical works is the I Ching, which greatly influenced written literature during the Zhou Dynasty (1050 BC-256 BC). For mathematics, the book included a sophisticated use of hexagrams.
Since the Shang period, the Chinese had already fully developed a decimal system. Since early times, Chinese understood basic arithmetic (which dominated far eastern history), algebra, equations, and negative numbers.[citation needed] Although the Chinese were more focused on arithmetic and advanced algebra for astronomical uses they were also the first to develop negative numbers, algebraic geometry (only Chinese geometry) and the usage of decimals.
Mathematics was one of the Six Arts, students were required to master during the Zhou Dynasty (1122 BC - 256 BC). Learning them all perfectly was required to be a perfect gentleman, or in the Chinese sense, a "Renaissance Man". Six Arts have their roots in the Confucian philosophy.
The oldest existent work on geometry in China comes from the philosophical Mohist canon of c. 330 BC, compiled by the followers of Mozi (470 BC-390 BC). The Mo Jing described various aspects of many fields associated with physical science, and provided a small wealth of information on mathematics as well. It provided an 'atomic' definition of the geometric point, stating that a line is separated into parts, and the part which has no remaining parts (i.e. cannot be divided into smaller parts) and thus forms the extreme end of a line is a point.
Much like Euclid's first and third definitions and Plato's 'beginning of a line', the Mo Jing stated that "a point may stand at the end (of a line) or at its beginning like a head-presentation in childbirth. (As to its invisibility) there is nothing similar to it." Similar to the atomists of Democritus, the Mo Jing stated that a point is the smallest unit, and cannot be cut in half, since 'nothing' cannot be halved. It stated that two lines of equal length will always finish at the same place,[4] while providing definitions for the comparison of lengths and for parallels, along with principles of space and bounded space. It also described the fact that planes without the quality of thickness cannot be piled up since they cannot mutually touch. The book provided definitions for circumference, diameter, and radius, along with the definition of volume.
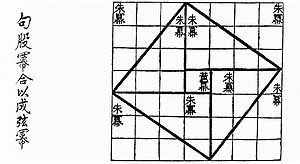
The history of mathematical development lacks some evidence. There are still debates about certain mathematical classics. For example, the Zhou Bi Suan Jing dates around 1200-1000BCE, yet many scholars believed it was written between 300-250BCE. The Zhou Bi Suan Jing contains an in depth proof of the Gougu Theorem (Pythagorean Theorem) but focuses more on astronomical calculations.
Not much is known about Qin dynasty mathematics, or before, due to the burning of books and burying of scholars.
Knowledge of this period must be carefully determined by their civil projects and historical evidence. The Qin dynasty created a standard system of weights. Civil projects of the Qin dynasty were incredible feats of human engineering. Emperor Qin Shihuang ordered many men to build large, lifesize statues for the palace, tomb along with various other temples and shrines. The shape of the tomb is designed with geometric skills of architecture. It is certain that one of the greatest feats of human history; the great wall required many mathematical "techniques." All Qin dynasty buildings and grand projects used advanced computation formulas for volume, area and proportion.
The Suan shu shu (writings on reckoning) is an ancient Chinese text on mathematics approximately seven thousand characters in length, written on 190 bamboo strips. It was discovered together with other writings in 1984 when archaeologists opened a tomb at Zhangjiashan in Hubei province. From documentary evidence this tomb is known to have been closed in 186 BC, early in the Western Han dynasty. While its relationship to the Nine Chapters is still under discussion by scholars, some of its contents are clearly paralleled there. The text of the Suan shu shu is however much less systematic than the Nine Chapters; and appears to consist of a number of more or less independent short sections of text drawn from a number of sources. Some linguistic hints point back to the Qin dynasty.
In an example of a elementary mathematics in the Suan shu shu, the square root is approximated by using an "excess and deficiency" method which says to "combine the excess and deficiency as the divisor; (taking) the deficiency numerator multiplied by the excess denominator and the excess numerator times the deficiency denominator, combine them as the dividend."
The Nine Chapters on the Mathematical Art is a Chinese mathematics book, its oldest archeological date being 179 AD (traditionally dated 1000BC), but perhaps as early as 300-200 BC. Although the author(s) are unknown, they made a huge contribution in the eastern world. The methods were made for everyday life and gradually taught advanced methods. It also contains evidence of the Gaussian elimination.
It was one of the most influential of all Chinese mathematical books and it is composed of some 246 problems. Chapter eight deals with solving determinate and indeterminate simultaneous linear equations using positive and negative numbers, with one problem dealing with solving four equations in five unknowns.
The earliest known magic squares appeared in China. In Nine Chapters the author solves a system of simultaneous linear equations by placing the coefficients and constant terms of the linear equations into a magic square (i.e. a matrix) and performing column reducing operations on the magic square.
In the third century Liu Hui wrote his commentary on the Nine Chapters and also wrote Haidao suanjing which dealt with using Pythagorean theorem (already known by the 9 chapters), and triangular measuration to measure the size of things. He discovered the usage of Cavalieri's principle to find an accurate formula for the volume of a cylinder, and also developed elements of the integral and the differential calculus during the 3rd century CE.
In the fourth century, another influential mathematician named Zu Chongzhi, introduced the Da Ming Li. This calendar was specifically calculated to predict many cosmological cycles that will occur in a period of time. Very little is really known about his life. Today, the only sources are found in the book Sui Shi, we now know that Zu Chongzhi was one of the generations of mathematicians. He computed the value of Pi till 7 accurate decimal places (between 3.1415926 and 3.1415927) and suggested 355/113 as a good approximate. Along with his son, Zu Geng, Zu Chongzhi used the Cavalieri Method to find an accurate solution for calculating the volume of the sphere. His work, Zhui Shu was discarded out of the syllabus of mathematics during the Song dynasty and lost. Many believed that Zhui Shu contains the formulas and methods for linear, matrix algebra, algorithm for calculating the value of Pi formula for the volume of the sphere. The text should also associate with his astronomical methods of interpolation, which would contain knowledge, similar to our modern mathematics.
In the fifth century the manual called "Zhang Qiujian suanjing" discussed linear and quadratic equations. By this point the Chinese had the concept of negative numbers.
By the Tang Dynasty study of math was fairly standard in the great schools.Wang Xiaotong was a great mathematician in the beginning of the Tang Dynasty, and he wrote a book: Jigu suanjing (Continuation of Ancient Mathematics).
The table of sines by the Indian mathematician, Aryabhata, were translated into the Chinese mathematical book of the Kaiyuan Zhanjing, compiled in 718 AD during the Tang Dynasty. Although the Chinese excelled in other fields of mathematics such as solid geometry, binomial theorem, and complex algebraic formulas, early forms of trigonometry were not as widely appreciated as in the contemporary Indian and Islamic mathematics. I-Xing, the mathematician and Buddhist monk was credited for calculating the tangent table. Instead, the early Chinese used an empirical substitute known as chong cha, while practical use of plane trigonometry in using the sine, the tangent, and the secant were known.
Four outstanding mathematicians arose during the Song Dynasty and Yuan Dynasty, particularly in the twelfth and thirteenth centuries: Yang Hui, Qin Jiushao, Li Zhi(Li Ye), and Zhu Shijie. Yang Hui, Qin Jiushao, Zhu Shijie all used the Horner-Ruffini method to solve certain types of simultaneous equations, roots, quadratic, cubic,and quartic equations. Yang Hui was also the first person in history to discover and prove "Pascal's Triangle", along with its binomial proof (although the earliest mention of the Pascal's triangle in China exists before the eleventh century C.E). Li Zhi on the other hand, investigated on a form of algebraic geometry.
His book; Ce Hai Yuan Jing revolutionized the idea of inscribing a circle into triangles, which could be calculated using equations with the Pythagorean theorem. Guo Shoujing of this era also worked on spherical trigonometry for precise astronomical calculations. At this point of mathematical history, a lot of modern western mathematics is already discovered by Chinese mathematicians.
Things grew quiet for a time until the thirteenth century Renaissance of Chinese math. This saw Chinese mathematicians solving equations with methods Europe would not know until the eighteenth century. The high point of this era came with Zhu Shijie's two books Suanxue qimeng and the Siyuan yujian. In one case he reportedly gave a method equivalent to Gauss's pivotal condensation.
Qin Jiushao (c. 1202Ð1261) was the first to introduce the zero symbol into Chinese mathematics. Before this innovation, blank spaces were used instead of zeros in the system of counting rods. Pascal's triangle was first illustrated in China by Yang Hui in his book Xiangjie Jiuzhang Suanfa, although it was described earlier around 1100 by Jia Xian. Although the Introduction to Computational Studies written by Zhu Shijie (fl. 13th century) in 1299 contained nothing new in Chinese algebra, it had a great impact on the development of Japanese mathematics.
Ts'e-yuan hai-ching, or Sea-Mirror of the Circle Measurements, is a collection of some 170 problems written by Li Chih (or Li Yeh) (1192 - 1272 A.D.). He used fan fa, or Horner's method, to solve equations of degree as high as six, although he did not describe his method of solving equations.
Shu-shu chiu-chang, or Mathematical Treatise in Nine Sections, was written by the wealthy governor and minister Ch'in Chiu-shao (ca. 1202 - ca. 1261 A.D.) and with the invention of a method of solving simultaneous congruences, it marks the high point in Chinese indeterminate analysis.
The earliest known magic squares of order greater than three are attributed to Yang Hui (fl. ca. 1261 - 1275), who worked with magic squares of order as high as ten.
The embryonic state of trigonometry in China slowly began to change and advance during the Song Dynasty (960-1279), where Chinese mathematicians began to express greater emphasis for the need of spherical trigonometry in calendarical science and astronomical calculations.
The polymath Chinese scientist, mathematician and official Shen Kuo (1031-1095) used trigonometric functions to solve mathematical problems of chords and arcs. Sal Restivo writes that Shen's work in the lengths of arcs of circles provided the basis for spherical trigonometry developed in the 13th century by the mathematician and astronomer Guo Shoujing (1231-1316). As the historians L. Gauchet and Joseph Needham state, Guo Shoujing used spherical trigonometry in his calculations to improve the calendar system and Chinese astronomy.
However after the overthrow of the Yuan Dynasty China became suspicious of knowledge it used. The Ming Dynasty turned away from math and physics in favor of botany and pharmacology. A revival of math in China began in the late nineteenth century, but this was largely based on Western modes of knowledge.
Despite the achievements of Shen and Guo's work in trigonometry, another substantial work in Chinese trigonometry would not be published again until 1607, with the dual publication of Euclid's Elements by Chinese official and astronomer Xu Guangqi (1562-1633) and the Italian Jesuit Matteo Ricci (1552-1610)
Chinese Mathematics Wikipedia