
People who have worked with alternative energy can tell you that it is often a long and tedious road to the completion of their projects but worth the "energy" they put in. It goes along with feeling one is doing something to help the planet, energy needs met in safer more efficient way. Geothermal energy - or anything having to do with drilling into the tectonic plates - is not a good way to go as many suspect fracking has caused the acceleration of earthquake activity in many parts of the world. All we can do is try and hope our efforts meet with success.
Alternative Energy is an umbrella term that refers to any source of usable energy intended to replace fuel sources without the undesired consequences of the replaced fuels. Typically, official uses of the term, such as qualification for governmental incentives, exclude fossil fuels and nuclear energy whose undesired consequences are high carbon dioxide emissions, the major contributing factor of global warming according to the Intergovernmental Panel on Climate Change, and difficulties of radioactive waste disposal. Over the years, the nature of what was regarded alternative energy sources has changed considerably, and today because of the variety of energy choices and differing goals of their advocates, defining some energy types as "alternative" is highly controversial.
The term "alternative" presupposes a set of undesirable energy technologies against which "alternative energies" are contrasted. As such, the list of energy technologies excluded is an indicator of which problems the alternative technologies are intended to address. Controversies regarding dominant sources of energy and their alternatives have a long history. The nature of what was regarded alternative energy sources has changed considerably over time, and today, because of the variety of energy choices and differing goals of their advocates, defining some energy types as "alternative" is highly controversial.
In a general sense in contemporary society, alternative energy is that which is produced without the undesirable consequences of the burning of fossil fuels, such as high carbon dioxide emissions, which is considered to be the major contributing factor of global warming according to the Intergovernmental Panel on Climate Change. Sometimes, this less comprehensive meaning of "alternative energy" excludes nuclear energy (e.g. as defined in the Michigan Next Energy Authority Act of 2002).
Solar energy is generating of electricity from the sun. It is split up into two types, thermal and electric energy. These two subgroups mean that they heat up homes (and water) and generate electricity respectively.
Wind energy is generating of electricity from the wind.
Geothermal energy is using hot water or steam from the Earth’s interior for heating buildings or electricity generation.
Biofuel and ethanol are plant-derived substitutes of gasoline for powering vehicles.
Hydrogen is used as clean fuel for airplanes, spaceships, and some cars.

How One Woman Helped Light Rural India With Solar Lamps National Geographic - July 20, 2015

She grew up in an affluent New York town but soon after college, Ajaita Shah went to her parents' native India to work with the poor.
Solar power is the conversion of sunlight into electricity, either directly using photovoltaics (PV), or indirectly using concentrated solar power (CSP). Concentrated solar power systems use lenses or mirrors and tracking systems to focus a large area of sunlight into a small beam. Photovoltaics convert light into electric current using the photoelectric effect.
Commercial concentrated solar power plants were first developed in the 1980s. The 354 MW SEGS CSP installation is the largest solar power plant in the world, located in the Mojave Desert of California. Other large CSP plants include the Solnova Solar Power Station (150 MW) and the Andasol solar power station (150 MW), both in Spain. The over 200 MW Agua Caliente Solar Project in the United States, and the 214 MW Charanka Solar Park in India, are the world’s largest photovoltaic plants.
Solar power is the conversion of sunlight into electricity. Sunlight can be converted directly into electricity using photovoltaics (PV), or indirectly with concentrated solar power (CSP), which normally focuses the sun's energy to boil water which is then used to provide power. Other technologies also exist, such as Stirling engine dishes which use a Stirling cycle engine to power a generator. Photovoltaics were initially used to power small and medium-sized applications, from the calculator powered by a single solar cell to off-grid homes powered by a photovoltaic array.
The primary obstacle that is preventing the large scale implementation of solar powered energy generation is the inefficiency of current solar technology. Currently, photovoltaic (PV) panels only have the ability to convert around 16% of the sunlight that hits them into electricity. At this rate, many experts believe that solar energy is not efficient enough to be economically sustainable given the cost to produce the panels themselves.
Both Sandia National Laboratories and the National Renewable Energy Laboratory (NREL), have heavily funded solar research programs. The NREL solar program has a budget of around $75 million and develops research projects in the areas of photovoltaic (PV) technology, solar thermal energy, and solar radiation. The budget for Sandia’s solar division is unknown, however it accounts for a significant percentage of the laboratory’s $2.4 billion budget.
Several academic programs have focused on solar research in recent years. The Solar Energy Research Center (SERC) at University of North Carolina (UNC) has the sole purpose of developing cost effective solar technology. In 2008, researchers at Massachusetts Institute of Technology (MIT) developed a method to store solar energy by using it to produce hydrogen fuel from water. Such research is targeted at addressing the obstacle that solar development faces of storing energy for use during nighttime hours when the sun is not shining.
In February of 2012, North Carolina-based Semprius Inc., a solar development company backed by German corporation Siemens, announced that they had developed the world's most efficient solar panel. The company claims that the prototype converts 33.9% of the sunlight that hits it to electricity, more than double the previous high-end conversion rate.

Wind power is the conversion of wind energy into a useful form of energy, such as using: wind turbines to make electricity, windmills for mechanical power, windpumps for water pumping or drainage, or sails to propel ships.
A large wind farm may consist of several hundred individual wind turbines which are connected to the electric power transmission network. Offshore wind farms can harness more frequent and powerful winds than are available to land-based installations and have less visual impact on the landscape but construction costs are considerably higher. Small onshore wind facilities are used to provide electricity to isolated locations and utility companies increasingly buy back surplus electricity produced by small domestic wind turbines.
Wind power, as an alternative to fossil fuels, is plentiful, renewable, widely distributed, clean, produces no greenhouse gas emissions during operation and uses little land. Any effects on the environment are generally less problematic than those from other power sources. As of 2011, 83 countries around the world are using wind power on a commercial basis.
As of 2010 wind energy was over 2.5% of total worldwide electricity usage, growing at more than 25% per annum. The monetary cost per unit of energy produced is similar to the cost for new coal and natural gas installations. Although wind power is a popular form of energy generation, the construction of wind farms is not universally welcomed due to aesthetics.
Although very consistent from year to year, wind power has significant variation over shorter timescales. The intermittency of wind seldom creates problems when used to supply up to 20% of total electricity demand, but as the proportion increases, a need to upgrade the grid, and a lowered ability to supplant conventional production can occur. Power management techniques such as having excess capacity storage, dispatchable backing supplies (usually natural gas), storage such as pumped-storage hydroelectricity, exporting and importing power to neighboring areas or reducing demand when wind production is low, can greatly mitigate these problems.
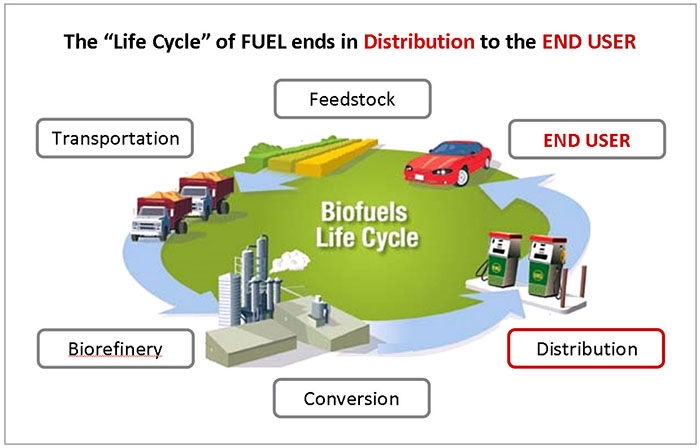
As the primary source of biofuels in North America, many organizations are conducting research in the area of ethanol production. On the Federal level, the USDA conducts a large amount of research regarding ethanol production in the United States. Much of this research is targeted toward the effect of ethanol production on domestic food markets.
The National Renewable Energy Laboratory has conducted various ethanol research projects, mainly in the area of cellulosic ethanol. Cellulosic ethanol has many benefits over traditional corn based-ethanol. It does not take away or directly conflict with the food supply because it is produced from wood, grasses, or non-edible parts of plants. Moreover, some studies have shown cellulosic ethanol to be more cost effective and economically sustainable than corn-based ethanol. Sandia National Laboratories conducts in-house cellulosic ethanol research and is also a member of the Joint BioEnergy Institute (JBEI), a research institute founded by the United States Department of Energy with the goal of developing cellulosic biofuels.
From 1978 to 1996, the National Renewable Energy Laboratory experimented with using algae as a biofuels source in the Aquatic Species Program. A self-published article by Michael Briggs, at the University of New Hampshire Biofuels Group, offers estimates for the realistic replacement of all motor vehicle fuel with biofuels by utilizing algae that have a natural oil content greater than 50%, which Briggs suggests can be grown on algae ponds at wastewater treatment plants. This oil-rich algae can then be extracted from the system and processed into biofuels, with the dried remainder further reprocessed to create ethanol.
The production of algae to harvest oil for biofuels has not yet been undertaken on a commercial scale, but feasibility studies have been conducted to arrive at the above yield estimate. In addition to its projected high yield, algaculture - unlike food crop-based biofuels - does not entail a decrease in food production, since it requires neither farmland nor fresh water. Many companies are pursuing algae bio-reactors for various purposes, including scaling up biofuels production to commercial levels.
Several groups in various sectors are conducting research on Jatropha curcas, a poisonous shrub-like tree that produces seeds considered by many to be a viable source of biofuels feedstock oil. Much of this research focuses on improving the overall per acre oil yield of Jatropha through advancements in genetics, soil science, and horticultural practices. SG Biofuels, a San Diego-based Jatropha developer, has used molecular breeding and biotechnology to produce elite hybrid seeds of Jatropha that show significant yield improvements over first generation varieties. The Center for Sustainable Energy Farming (CfSEF) is a Los Angeles-based non-profit research organization dedicated to Jatropha research in the areas of plant science, agronomy, and horticulture. Successful exploration of these disciplines is projected to increase Jatropha farm production yields by 200-300% in the next ten years.

Geothermal energy is thermal energy generated and stored in the Earth. Thermal energy is the energy that determines the temperature of matter. The Geothermal energy of the Earth's crust originates from the original formation of the planet (20%) and from radioactive decay of minerals (80%).The geothermal gradient, which is the difference in temperature between the core of the planet and its surface, drives a continuous conduction of thermal energy in the form of heat from the core to the surface.
At the core of the Earth, thermal energy is created by radioactive decay and temperatures may reach over 5000 degrees Celsius (9,000 degrees Fahrenheit). Heat conducts from the core to surrounding cooler rock. The high temperature and pressure cause some rock to melt, creating magma convection upward since it is lighter than the solid rock. The magma heats rock and water in the crust, sometimes up to 370 degrees Celsius (700 degrees Fahrenheit).
From hot springs, geothermal energy has been used for bathing since Paleolithic times and for space heating since ancient Roman times, but it is now better known for electricity generation. Worldwide, about 10,715 megawatts (MW) of geothermal power is online in 24 countries. An additional 28 gigawatts of direct geothermal heating capacity is installed for district heating, space heating, spas, industrial processes, desalination and agricultural applications.
Geothermal power is cost effective, reliable, sustainable, and environmentally friendly, but has historically been limited to areas near tectonic plate boundaries. Recent technological advances have dramatically expanded the range and size of viable resources, especially for applications such as home heating, opening a potential for widespread exploitation. Geothermal wells release greenhouse gases trapped deep within the earth, but these emissions are much lower per energy unit than those of fossil fuels. As a result, geothermal power has the potential to help mitigate global warming if widely deployed in place of fossil fuels.
The Earth's geothermal resources are theoretically more than adequate to supply humanity's energy needs, but only a very small fraction may be profitably exploited. Drilling and exploration for deep resources is very expensive. Forecasts for the future of geothermal power depend on assumptions about technology, energy prices, subsidies, and interest rates. Polls show that customers would be willing to pay a little more for a renewable energy source like geothermal. But as a result of government assisted research and industry experience, the cost of generating geothermal power has decreased by 25% over the past two decades In 2001, geothermal energy cost between two and ten cents per kwh.
Over $1 billion of federal money has been spent on the research and development of hydrogen fuel in the United States. Both the National Renewable Energy Laboratory and Sandia National Laboratories have departments dedicated to hydrogen research.
Renewable energy is generated from natural resources - such as sunlight, wind, rain, tides and geothermal heat - which are renewable (naturally replenished). When comparing the processes for producing energy, there remain several fundamental differences between renewable energy and fossil fuels. The process of producing oil, coal, or natural gas fuel is a difficult and demanding process that requires a great deal of complex equipment, physical and chemical processes. On the other hand, alternative energy can be widely produced with basic equipment and naturally basic processes. Wood, the most renewable and available alternative energy, burns the same amount of carbon it would emit if it degraded naturally.
Renewable energy sources such as biomass are sometimes regarded as an alternative to ecologically harmful fossil fuels. Renewables are not inherently alternative energies for this purpose. For example, the Netherlands, once leader in use of palm oil as a biofuel, has suspended all subsidies for palm oil due to the scientific evidence that their use "may sometimes create more environmental harm than fossil fuels".
The Netherlands government and environmental groups are trying to trace the origins of imported palm oil, to certify which operations produce the oil in a responsible manner. Regarding biofuels from foodstuffs, the realization that converting the entire grain harvest of the US would only produce 16% of its auto fuel needs, and the decimation of Brazil's CO2 absorbing tropical rain forests to make way for biofuel production has made it clear that placing energy markets in competition with food markets results in higher food prices and insignificant or negative impact on energy issues such as global warming or dependence on foreign energy. Recently, alternatives to such undesirable sustainable fuels are being sought, such as commercially viable sources of cellulosic ethanol.
Algae fuel is a biofuel which is derived from algae. During photosynthesis, algae and other photosynthetic organisms capture carbon dioxide and sunlight and convert it into oxygen and biomass. The benefits of algal biofuel are that it can be produced industrially, thereby obviating the use of arable land and food crops (such as soy, palm, and canola), and that it has a very high oil yield as compared to all other sources of biofuel.
Biomass briquettes are being developed in the developing world as an alternative to charcoal. The technique involves the conversion of almost any plant matter into compressed briquettes that typically have about 70% the calorific value of charcoal. There are relatively few examples of large scale briquette production. One exception is in North Kivu, in eastern Democratic Republic of Congo, where forest clearance for charcoal production is considered to be the biggest threat to Mountain Gorilla habitat. The staff of Virunga National Park have successfully trained and equipped over 3500 people to produce biomass briquettes, thereby replacing charcoal produced illegally inside the national park, and creating significant employment for people living in extreme poverty in conflict affected areas.
Biogas digestion deals with harnessing the methane gas that is released when waste breaks down. This gas can be retrieved from garbage or sewage systems. Biogas digesters are used to process methane gas by having bacteria break down biomass in an anaerobic environment. The methane gas that is collected and refined can be used as an energy source for various products.
Biological Hydrogen Production -- Hydrogen gas is a completely clean burning fuel; its only by-product is water. It also contains relatively high amount of energy compared with other fuels due to its chemical structure. This requires a high-energy input, making commercial hydrogen very inefficient.
Use of a biological vector as a means to split water, and therefore produce hydrogen gas, would allow for the only energy input to be solar radiation. Biological vectors can include bacteria or more commonly algae. This process is known as biological hydrogen production. It requires the use of single celled organisms to create hydrogen gas through fermentation. Without the presence of oxygen, also known as an anaerobic environment, regular cellular respiration cannot take place and a process known as fermentation takes over. A major by-product of this process is hydrogen gas. If we could implement this on a large scale, then we could take sunlight, nutrients and water and create hydrogen gas to be used as a dense source of energy.
Large-scale production has proven difficult. It was not until 1999 that we were able to even induce these anaerobic conditions by sulfur deprivation. Since the fermentation process is an evolutionary back up, turned on during stress, the cells would die after a few days. In 2000, a two-stage process was developed to take the cells in and out of anaerobic conditions and therefore keep them alive. For the last ten years, finding a way to do this on a large-scale has been the main goal of research. Careful work is being done to ensure an efficient process before large-scale production, however once a mechanism is developed, this type of production could solve our energy needs.
Floating wind farms are similar to a regular wind farm, but the difference is that they float in the middle of the ocean. Offshore wind farms can be placed in water up to 40 metres (130 ft) deep, whereas floating wind turbines can float in water up to 700 metres (2,300 ft) deep. The advantage of having a floating wind farm is to be able to harness the winds from the open ocean. Without any obstructions such as hills, trees and buildings, winds from the open ocean can reach up to speeds twice as fast as coastal areas.
Over the last three years publicly traded alternative energy have been very volatile, with some 2007 returns in excess of 100%, some 2008 returns down 90% or more, and peak-to-trough returns in 2009 again over 100%. In general there are three subsegments of “alternative” energy investment: solar energy, wind energy and hybrid electric vehicles. Alternative energy sources which are renewable, free and have lower carbon emissions than what we have now are wind energy, solar energy, geothermal energy, and bio fuels. Each of these four segments involve very different technologies and investment concerns.
For example, photovoltaic solar energy is based on semiconductor processing and accordingly, benefits from steep cost reductions similar to those realized in the microprocessor industry (i.e., driven by larger scale, higher module efficiency, and improving processing technologies). PV solar energy is perhaps the only energy technology whose electricity generation cost could be reduced by half or more over the next 5 years. Better and more efficient manufacturing process and new technology such as advanced thin film solar cell is a good example of that helps to reduce industry cost.
The economics of solar PV electricity are highly dependent on silicon pricing and even companies whose technologies are based on other materials (e.g., First Solar) are impacted by the balance of supply and demand in the silicon market.In addition, because some companies sell completed solar cells on the open market (e.g., Q-Cells), this creates a low barrier to entry for companies that want to manufacture solar modules, which in turn can create an irrational pricing environment.
In contrast, because wind power has been harnessed for over 100 years, its underlying technology is relatively stable. Its economics are largely determined by siting (e.g., how hard the wind blows and the grid investment requirements) and the prices of steel (the largest component of a wind turbine) and select composites (used for the blades). Because current wind turbines are often in excess of 100 meters high, logistics and a global manufacturing platform are major sources of competitive advantage. These issues and others were explored in a research report by Sanford Bernstein. Some of its key conclusions are shown here.
Due to steadily rising gas prices in 2008 with the US national average price per gallon of regular unleaded gas rising above $4.00 at one point, there has been a steady movement towards developing higher fuel efficiency and more alternative fuel vehicles for consumers. In response, many smaller companies have rapidly increased research and development into radically different ways of powering consumer vehicles. Hybrid and battery electric vehicles are commercially available and are gaining wider industry and consumer acceptance worldwide.
Before alternative energy becomes main-stream there are a few crucial obstacles that it must overcome: First there must be increased understanding of how alternative energies work and why they are beneficial; secondly the availability components for these systems must increase; and lastly the pay-off time must be decreased.
For example, electric vehicles (EV) and Plug-in Hybrid Electric Vehicles (PHEV) are on the rise. These vehicles depend heavily on an effective charging infrastructure such as a smart grid infrastructure to be able to implement electricity as mainstream alternative energy for future transportations.
There are numerous organizations within the academic, federal, and commercial sectors conducting large scale advanced research in the field of alternative energy. This research spans several areas of focus across the alternative energy spectrum. Most of the research is targeted at improving efficiency and increasing overall energy yields.
Multiple federally supported research organizations have focused on alternative energy in recent years. Two of the most prominent of these labs are Sandia National Laboratories and the National Renewable Energy Laboratory (NREL), both of which are funded by the United States Department of Energy and supported by various corporate partners. Sandia has a total budget of $2.4 billion while NREL has a budget of $375 million.
There are a number of issues that may arise from switching to alternative energy. Increasing the nation's use of natural gas for electricity generation could result in adverse economic consequences, especially since natural gas currently costs about four times more than coal.
Furthermore, if there were a widespread switching to natural gas from coal some countries would become increasingly dependent on international supplies. Also, large-scale fuel switching would require substantial investments in pipeline storage and storage capacity and new terminals to process imported natural gas. There is also the question of whether to convert existing coal-burning plants or to construct new ones. Burning natural gas at an existing coal plant would require a pipeline with the ability to meet the plant's fuel supply requirements. It would also require expansion of interstate and intrastate pipelines to transport increased volumes of natural gas. Overall it would be more feasible and cost-effective to construct new natural gas units than to switch coal-burning plants.
Sustainable energy is the sustainable provision of energy that meets the needs of the present without compromising the ability of future generations to meet their needs. Technologies that promote sustainable energy include renewable energy sources, such as hydroelectricity, solar energy, wind energy, wave power, geothermal energy, and tidal power, and also technologies designed to improve energy efficiency.