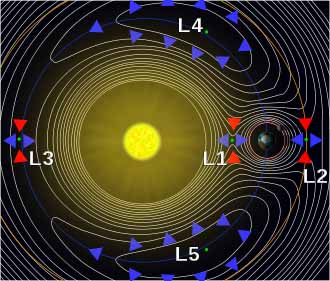
Lagrange Points also L-points, are the five positions in an orbital configuration where a small object affected only by gravity can theoretically be stationary relative to two larger objects (such as a satellite with respect to the Earth and Moon). The Lagrange points mark positions where the combined gravitational pull of the two large masses provides precisely the centripetal force required to rotate with them. They are analogous to geostationary orbits in that they allow an object to be in a "fixed" position in space rather than an orbit in which its relative position changes continuously.

Lagrangian points are the stationary solutions of the circular restricted three-body problem. For example, given two massive bodies in circular orbits around their common center of mass, there are five positions in space where a third body, of comparatively negligible mass, could be placed which would then maintain its position relative to the two massive bodies. As seen in a rotating reference frame with the same period as the two co-orbiting bodies, the gravitational fields of two massive bodies combined with the satellite's circular motion are in balance at the Lagrangian points, allowing the third body to be stationary with respect to the first two bodies. P> The three collinear Lagrange points were first discovered by Leonhard Euler around 1750.

In 1772, the Italian-French mathematician Joseph Louis Lagrange was working on the famous three-body problem when he discovered an interesting quirk in the results. Originally, he had set out to discover a way to easily calculate the gravitational interaction between arbitrary numbers of bodies in a system, because Newtonian mechanics concludes that such a system results in the bodies orbiting chaotically until there is a collision, or a body is thrown out of the system so that equilibrium can be achieved.

The logic behind this conclusion is that a system with one body is trivial, as it is merely static relative to itself; a system with two bodies is the relatively simple two-body problem, with the bodies orbiting around their common center of mass. However, once more than two bodies are introduced, the mathematical calculations become very complicated. A situation arises where you would have to calculate every gravitational interaction between every pair of objects at every point along its trajectory.

Lagrange, however, wanted to make this simpler. He did so with a simple hypothesis: The trajectory of an object is determined by finding a path that minimizes the action over time. This is found by subtracting the potential energy from the kinetic energy. With this way of thinking, Lagrange re-formulated the classical Newtonian mechanics to give rise to Lagrangian mechanics. With his new system of calculations, LagrangeÕs work led him to hypothesize how a third body of negligible mass would orbit around two larger bodies which were already in a near-circular orbit.

In a frame of reference that rotates with the larger bodies, he found five specific fixed points where the third body experiences zero net force as it follows the circular orbit of its host bodies (planets). These points were named ÒLagrangian pointsÓ in Lagrange's honor. It took over a hundred years before his mathematical theory was observed with the discovery of the Trojan asteroids at the Lagrange points of the SunÐJupiter system in 1906.

In the more general case of elliptical orbits, there are no longer stationary points in the same sense: it becomes more of a Lagrangian ÒareaÓ. The Lagrangian points constructed at each point in time, as in the circular case, form stationary elliptical orbits which are similar to the orbits of the massive bodies. Lagrange Points Wikipedia