



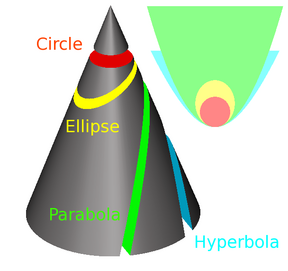
Apollonius of Perga [Pergaeus] (ca. 262 BC - ca. 190 BC) was a Greek geometer and astronomer, of the Alexandrian school, noted for his writings on conic sections. It was Apollonius who gave the ellipse, the parabola, and the hyperbola the names by which we know them.
The hypothesis of eccentric orbits, or equivalently, deferent and epicycles, to explain the apparent motion of the planets and the varying speed of the Moon, are also attributed to him. He was probably born twenty-five years later than Archimedes, i.e. about 262 B.C.
He flourished in the reigns of Ptolemy Euergetes and Ptolemy Philopator (247-205 B.C.). His treatise on Conics gained him the title of The Great Geometer, and is that by which his fame has been transmitted to modern times.
All his numerous other treatises have perished, save one, and we have only their titles handed down, with general indications of their contents, by later writers, especially Pappus. After the Conics in eight Books had been written in a first edition, Apollonius brought out a second edition, considerably revised as regards Books i.-ii., at the instance of one Eudemus of Pergamum; the first three books were sent to Eudemus at intervals, as revised, and the later books were dedicated (after Eudemus' death) to King Attalus I. (241-197 B.C.).
Only four Books have survived in Greek; three more are extant in Arabic; the eighth has never been found. Although a fragment has been found of a Latin translation from the Arabic made in the 13th century, it was not until 1661 that a Latin translation of Books v.-vii. was available.
This was made by Giovanni Alfonso Borelli and Abraham Ecchellensis from the free version in Arabic made in 983 by Abu 'l-Fath of Ispahan and preserved in a Florence MS. But the best Arabic translation is that made as regards Books i.-iv. by Hilal ibn Abi Hilal (d. about 883), and as regards Books v.-vii. by Tobit ben Korra (836-901).
Halley used for his translation an Oxford MS. of this translation of Books v.-vii., but the best MS. (Bodl. 943) he only referred to in order to correct his translation, and it is still unpublished except for a fragment of Book v. published by L. Nix with German translation (Drugulin, Leipzig, 1889).
Halley added in his edition (1710) a restoration of Book viii., in which he was guided by the fact that Pappus gives lemmas "to the seventh and eighth books" under that one heading, as well as by the statement of Apollonius himself that the use of the seventh book was illustrated by the problems solved in the eighth.
The degree of originality of the Conics can best be judged from Apollonius' own prefaces. Books i.-iv. form an "elementary introduction," i.e. contain the essential principles; the rest are specialized investigations in particular directions.
For Books i.-iv. he claims only that the generation of the curves and their fundamental properties in Book i. are worked out more fully and generally than they were in earlier treatises, and that a number of theorems in Book iii. and the greater part of Book iv. are new.
That he made the fullest use of his predecessors' works, such as Euclid's four Books on Conics, is clear from his allusions to Euclid, Conon and Nicoteles.
The generality of treatment is indeed remarkable; he gives as the fundamental property of all the conics the equivalent of the Cartesian equation referred to oblique axes (consisting of a diameter and the tangent at its extremity) obtained by cutting an oblique circular cone in any manner, and the axes appear only as a particular case after he has shown that the property of the conic can be expressed in the same form with reference to any new diameter and the tangent at its extremity.
It is clearly the form of the fundamental property (expressed in the terminology of the "application of areas") which led him to call the curves for the first time by the names parabola, ellipse, hyperbola. Books v.-vii. are clearly original.
Apollonius' genius takes its highest flight in Book v., where he treats of normals as minimum and maximum straight lines drawn from given points to the curve (independently of tangent properties), discusses how many normals can be drawn from particular points, finds their feet by construction, and gives propositions determining the centre of curvature at any point and leading at once to the Cartesian equation of the evolute of any conic. Apollonius of Perga